Line-Fit sur PC image

Télécharger Line-Fit sur PC


  • Catégorie: Productivity
  • Version actuelle: 2.0
  • Dernière mise à jour: 2020-11-15
  • Taille du fichier: 670.00 kB
  • Développeur: Bjarne Berge
  • Compatibility: Requis Windows 11, Windows 10, Windows 8 et Windows 7

Télécharger l'APK compatible pour PC


Télécharger pour Android Développeur Rating Score Version actuelle Classement des adultes
↓ Télécharger pour Android Bjarne Berge 0 0 2.0 4+

Line-Fit pour PC: Comment télécharger et installer sur un PC Windows

                   


Bonne nouvelle! Une application Windows comme Line-Fit est disponible! Télécharger ci-dessous:

SN App Télécharger Rating Développeur
1. Gambino Slots Online 777 Games: Free Casino Slot Machines Gambino Slots Online 777 Games: Free Casino Slot Machines Télécharger 4.7/5
1,062 Commentaires 		Spiral Interactive
2. Solitaire Online JD Solitaire Online JD Télécharger 4.5/5
564 Commentaires 		Jimmy Dickinson
3. Gangstar New Orleans: Online Open World Game Gangstar New Orleans: Online Open World Game Télécharger 3.8/5
536 Commentaires 		Gameloft.
Sinon, suivez les instructions ci-dessous pour utiliser Line-Fit sur PC:

En 4 étapes, je vais vous montrer comment télécharger et installer Line-Fit sur votre ordinateur :


1: Téléchargez un logiciel d'émulation

Un émulateur imite/émule un appareil Android sur votre PC Windows, ce qui facilite l'installation d'applications Android sur votre ordinateur. Pour commencer, vous pouvez choisir l'un des émulateurs populaires ci-dessous:

  1. Nox App
  2. Bluestacks
Windowsapp.fr recommande Bluestacks - un émulateur très populaire avec des tutoriels d'aide en ligne


2 : Installez le logiciel de l'émulateur sur votre ordinateur

Si Bluestacks.exe ou Nox.exe a été téléchargé avec succès, accédez au dossier "Téléchargements" sur votre ordinateur ou n'importe où l'ordinateur stocke les fichiers téléchargés.

  1. Une fois trouvé, cliquez dessus. Le processus d'installation va commencer.
  2. Acceptez les conditions d'utilisation/le contrat de licence et suivez les instructions à l'écran.


3: Installez Line-Fit sur PC à l'aide de l'application Emulator

Lorsque l'émulateur est installé, ouvrez l'application et saisissez Line-Fit dans la barre de recherche ; puis appuyez sur rechercher. Vous verrez facilement l'application que vous venez de rechercher. Clique dessus. Il affichera Line-Fit dans votre logiciel émulateur. Appuyez sur le bouton "installer" et l'application commencera à s'installer.


Line-Fit Sur iTunes


Télécharger Développeur Rating Score Version actuelle Classement des adultes
Gratuit Sur iTunes Bjarne Berge 0 0 2.0 4+

Line-Fit Logiciel Aperçu

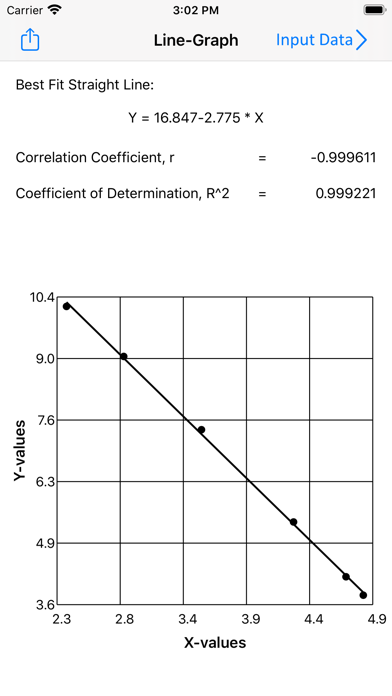
The Line-Fit app uses linear regression to model the relationship between two variables (x and y) by fitting a linear equation to observed data.  A linear regression line has an equation of the form Y = a + bX, where X is the explanatory variable and Y is the dependent variable.  To measure the association between the two variables the correlation coefficient is used, which is a value between -1 and 1 indicating the strength of the association of the observed data for the two variables.  The coefficient of determination, R2, measures how close the data are to the fitted regression line.  One variable is considered to be an explanatory (independent) variable, and the other is considered to be a response (dependent) variable.  In general, higher values of R2 indicate a better fit of the model to the given data.  The slope of the line is b, and the intercept is a (the value of y when x = 0).  R2 is always positive and equal to 1.0 for a perfect fit. 

Plus d'applications comme Line-Fit



Toutes les applications par Bjarne Berge

keyboard_arrow_up