Curve-Fit sur PC image

Télécharger Curve-Fit sur PC


  • Catégorie: Utilities
  • Version actuelle: 6.0
  • Dernière mise à jour: 2020-11-23
  • Taille du fichier: 790.00 kB
  • Développeur: Bjarne Berge
  • Compatibility: Requis Windows 11, Windows 10, Windows 8 et Windows 7

Télécharger l'APK compatible pour PC


Télécharger pour Android Développeur Rating Score Version actuelle Classement des adultes
↓ Télécharger pour Android Bjarne Berge 0 0 6.0 4+

Curve-Fit pour PC: Comment télécharger et installer sur un PC Windows

                   

Rechercher des applications PC compatibles ou des alternatives


Logiciel Télécharger Rating Développeur
pour PC 2 Curve-Fit Obtenez l'app PC 0/5
0 la revue
0
 Bjarne Berge

Sinon, suivez les instructions ci-dessous pour utiliser Curve-Fit sur PC:

En 4 étapes, je vais vous montrer comment télécharger et installer Curve-Fit sur votre ordinateur :


1: Téléchargez un logiciel d'émulation

Un émulateur imite/émule un appareil Android sur votre PC Windows, ce qui facilite l'installation d'applications Android sur votre ordinateur. Pour commencer, vous pouvez choisir l'un des émulateurs populaires ci-dessous:

  1. Nox App
  2. Bluestacks
Windowsapp.fr recommande Bluestacks - un émulateur très populaire avec des tutoriels d'aide en ligne


2 : Installez le logiciel de l'émulateur sur votre ordinateur

Si Bluestacks.exe ou Nox.exe a été téléchargé avec succès, accédez au dossier "Téléchargements" sur votre ordinateur ou n'importe où l'ordinateur stocke les fichiers téléchargés.

  1. Une fois trouvé, cliquez dessus. Le processus d'installation va commencer.
  2. Acceptez les conditions d'utilisation/le contrat de licence et suivez les instructions à l'écran.


3: Installez Curve-Fit sur PC à l'aide de l'application Emulator

Lorsque l'émulateur est installé, ouvrez l'application et saisissez Curve-Fit dans la barre de recherche ; puis appuyez sur rechercher. Vous verrez facilement l'application que vous venez de rechercher. Clique dessus. Il affichera Curve-Fit dans votre logiciel émulateur. Appuyez sur le bouton "installer" et l'application commencera à s'installer.


Curve-Fit Sur iTunes


Télécharger Développeur Rating Score Version actuelle Classement des adultes
Gratuit Sur iTunes Bjarne Berge 0 0 6.0 4+

Curve-Fit Logiciel Aperçu

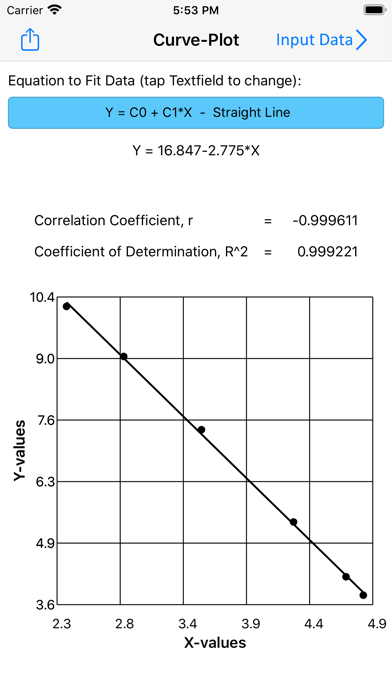
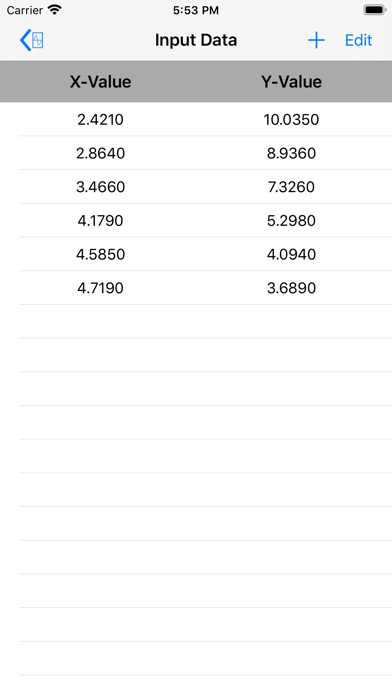
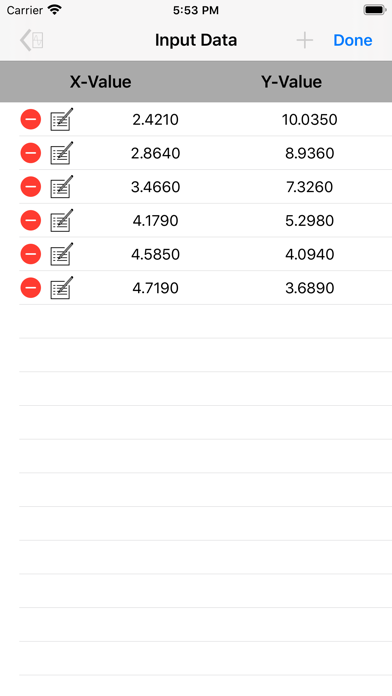
The constants are determined to minimize the sum of squares of the differences between the measured values (Y1, Y2, - - - , Yn) and the predicted equation Yc = F(X) which is found by curve-fitting the given data.  'cette application' uses regression analysis by the method of least squares to find best fit for a set of data to a selected equation.  The curve-fitting technique used in this app is based on regression analysis by the method of least squares.  Most literature deals with least squares analysis for straight lines, 2nd degree polynomials, and functions that can be linearized.  The free version fits a straight line through a data-set using least squares analysis.  Thereby there will be generated as many algebraic equations as given data points, and the number of equations will be larger than unknowns.  These types of equations are applicable for least-squares regression.  The input-data is transformed into a format that the can be put into linear forms with undetermined constants.  This is done by letting the derivative of the above equation equal zero. 

Plus d'applications comme Curve-Fit



Toutes les applications par Bjarne Berge

keyboard_arrow_up